ഈ പോസ്റ്റില് നമുക്ക് നക്ഷത്ര ദൃഗ്ഭ്രംശം അഥവാ Stellar Parallax എന്നാല് എന്താണെന്നും അതിനു ജ്യോതിശാസ്ത്രത്തിലുള്ള പ്രാധാന്യത്തെകുറിച്ചും മനസ്സിലാക്കാം. പാര്സെക്കിനെ കുറിച്ചുള്ള പോസ്റ്റില് ആ ഏകകത്തിനു പാരലാക്സുമായി ബന്ധമുണ്ട് എന്ന് പറഞ്ഞിരുന്നു. എങ്ങനെയാണ് അത് പാരലാക്സുമായി ബന്ധപ്പെട്ടിരിക്കുന്നത് എന്നും ഈ പോസ്റ്റില് വിശദീകരിച്ചിരിക്കുന്നു.
എന്താണ് ദൃഗ്ഭ്രംശം അഥവാ Parallax?
വളരെ ലളിതമായി പറഞ്ഞാല് ഒരു വസ്തുവിനെ രണ്ട് വ്യത്യസ്ത സ്ഥലങ്ങളില് നിന്ന് വീക്ഷിക്കുമ്പോള് ആ വസ്തുവിന്റെ സ്ഥാനത്തിനുണ്ടാകുന്ന ആപേക്ഷികമായ ചലനത്തെ ആണ് ദൃഗ്ഭ്രംശം എന്ന് പറയുന്നത്.
ഈ പ്രതിഭാസം മനസ്സിലാക്കാന് നമുക്ക് നിത്യജീവിതത്തില് പരിചയമുള്ള ഒരു ഉദാഹരണം ചൂണ്ടികാണിക്കട്ടെ. വളരെ കൃത്യമായ ഒരു ഉദാഹരണം അല്ലെങ്കിലും ദൃഗ്ഭ്രംശം എന്താണെന്ന് മനസ്സിലാക്കാന് ഈ ഉദാഹരണം നിങ്ങളെ സഹായിക്കും. കൈ നീട്ടി നിങ്ങളുടെ തള്ള വിരല് മുഖത്തിനു നേരെ പിടിക്കുക. എന്നിട്ട് ഇടത്തേ കണ്ണ് അടച്ച് നിങ്ങള് നിങ്ങളുടെ തള്ളവിരലിനെ കുറച്ചുദൂരെയുള്ള വസ്തുക്കളെ പശ്ചാത്തലമാക്കി നോക്കുക. ഇനി ഇടത്തേ കണ്ണ് തുറന്ന് വലത്തേ കണ്ണ് അടച്ച് നിങ്ങളുടെ തള്ളവിരലിനെ ദൂരെയുള്ള വസ്തുക്കളെ പശ്ചാത്തലമാക്കി നോക്കുക. ഇനി ഈ പ്രവര്ത്തനം കുറച്ചു വേഗത്തില് ചെയ്യുക. അപ്പോള് നിങ്ങള്ക്ക് നിങ്ങളുടെ തള്ളവിരല് ഇടത്തോട്ടും വലത്തോട്ടും ആയി മാറി കളിക്കുന്നത് കാണാം. ഈ പ്രതിഭാസത്തിനാണ് ദൃഗ്ഭ്രംശം(Parallax) എന്നു പറയുന്നത്. നിങ്ങള്ക്ക് നിങ്ങളുടെ രണ്ടു കണ്ണിന്റേയും ഇടയില് ഉള്ള ദൂരവും നിങ്ങളുടെ തള്ള വിരല് നിങ്ങളുടെ കണ്ണുകളില് ചെലുത്തുന്ന കോണീയ അളവും അറിയാമെങ്കില് നിങ്ങളുടെ കണ്ണുകളില് നിന്ന് തള്ളവിരലിലേക്കുള്ള ദൂരം കൃത്യമായി കണ്ടുപിടിക്കാം. ഇത് എങ്ങനെയാണെന്ന് നോക്കാം. താഴെയുള്ള ചിത്രം നോക്കൂ.
നിങ്ങളുടെ കണ്ണുകള്ക്കിടയിലുള്ള ദൂരം b-യും, വസ്തുവിലേക്കുള്ള (ഇവിടെ തള്ള വിരല്) ദൂരം d-യും നിങ്ങള് മാറി മാറി കണ്ണടച്ച് തുറന്നത് മൂലം ഉണ്ടായ ദൃഗ്ഭ്രംശം ഉണ്ടാക്കിയ കോണീയ അളവ് p എന്നും ഇരിക്കട്ടെ. ഈ മൂന്ന് പരിണാമങ്ങളും ത്രികോണമിതിയിലെ tangent മായി താഴെ കാണുന്ന സമവാക്യ പ്രകാരം ബന്ധപ്പെട്ടിരിക്കുന്നു.
tan(p/2) = (b/2)/d
ഒന്നു പുനഃക്രമീകരിച്ച് എഴുതിയാല് d-യുടെ മൂല്യം കണക്കാക്കാനുള്ള സമവാക്യം കിട്ടുന്നു.
d = (b/2)/tan(p/2)
ചുരുക്കത്തില് നിങ്ങള്ക്ക് നിങ്ങളുടെ കണ്ണുകളുടെ ഇടയിലുള്ള ദൂരവും ദൃഗ്ഭ്രംശം ഉണ്ടാക്കിയ കോണീയ അളവും കൃത്യമായി അറിയാമെങ്കില് വസ്തുവിലേക്കുള്ള ദൂരം കൃത്യമായി കണക്കാക്കാം.
നക്ഷത്ര ദൃഗ്ഭ്രംശം അഥവാ Stellar parallax
ജ്യോതിശാസ്ത്രജ്ഞന്മാര് ഈ ലളിതമായ പ്രതിഭാസം ഉപയോഗിച്ച് നക്ഷത്രങ്ങളിലേക്കും മറ്റുമുള്ള ദൂരം അളക്കുന്നു. ഈ മാര്ഗ്ഗ പ്രകാരം വസ്തുവിലേക്കുള്ള ദൂരം അളക്കുമ്പോള് രണ്ട് നിരീക്ഷണ സ്ഥാനവും തമ്മില് എത്ര അധികം ദൂരം കൂടുന്നുവോ അത്ര അധികം കൃത്യതയും കൂടും. നമ്മള് ഭൂമിയില് നിന്ന് നിരീക്ഷിക്കുമ്പോള് ഏറ്റവും അധികം ദൂരത്തു കിട്ടാവുന്ന രണ്ട് നിരീക്ഷണ സ്ഥാനങ്ങള് സൂര്യനു ചുറ്റുമുള്ള ഭൂമിയുടെ ഭ്രമണ പാതയില് 6 മാസത്തിന്റെ ഇടവേളയില് വരുന്ന രണ്ട് സ്ഥാനങ്ങള് ആണ്. ഈ രണ്ട് സ്ഥാനങ്ങളില് നിന്ന് നിരീക്ഷിക്കുമ്പോള് മുകളില് പറഞ്ഞ ഉദാഹരണം പോലെ ചില സമീപ നക്ഷത്രങ്ങള് അതിവിദൂരതയില് ഉള്ള നക്ഷത്രങ്ങളെ പശ്ചാത്തലമാക്കി അങ്ങോട്ടും ഇങ്ങോട്ടും നീങ്ങുന്നതായി നമുക്ക് തോന്നുന്നു. ഇതിനാണ് നക്ഷത്ര ദൃഗ്ഭ്രംശം അഥവാ Stellar Parallax എന്നു പറയുന്നത്.
1 AU ദൂരത്തുള്ള രണ്ട് ബിന്ദുക്കളില് നിന്ന് നോക്കുമ്പോള് നമുക്ക് കിട്ടുന്ന ക്ഭ്രംശകോണിനെ (parallax angle) ആണ് ജ്യോതിശാസ്ത്രത്തിലെ ഔദ്യോഗിക ദൃഗ്ഭ്രംശകോണ്. പക്ഷെ കൃത്യതയ്ക്കു വേണ്ടി 2 AU ദൂരത്തുനിന്നുള്ള രണ്ട് ബിന്ദുക്കളില് നിന്ന് ദൃഗ്ഭ്രംശകോണ് അളന്ന് അതിന്റെ പകുതി എടുക്കുന്നു.
ജ്യോതിശാസ്ത്രത്തില് ഉപയോഗിക്കുന്ന ഏകകങ്ങള്- ഭാഗം I എന്ന പോസ്റ്റില് സുനില് എന്ന ബ്ലോഗ്ഗര് പ്രസക്തമായ ഒരു ചോദ്യം ചോദിച്ചു. ചോദ്യം ഇതാണ്. Sunil said... I read in one book that about parcec.In that when we look a star/an object in an interval of 6 months, if we get a change of 1 arc second. THis means that object is one Parcec Away.. But 6 months interval means we are 2 Astronomical Unit away from the first place.. I think you have to change the 1 arc second in your picture to 0.5 Arc Second
അന്ന് പാരലാക്സിനെ കുറിച്ച് വിശദീകരിക്കാത്തതു കൊണ്ട് അദ്ദേഹത്തിനു തൃപ്തികരമായ ഒരു ഉത്തരം നല്കാന് ആയില്ല. മുകളിലത്തെ വിശദീകരണം അദ്ദേഹത്തിന്റെ ചോദ്യത്തിനുള്ള ഉത്തരം നല്കുന്നു. അതായത് 1 AU ദൂരത്തുള്ള രണ്ട് ബിന്ദുക്കളില് നിന്ന് നോക്കുമ്പോള് നമുക്ക് കിട്ടുന്ന ദൃഗ്ഭ്രംശകോണ് (parallax angle) ആണ് ജ്യോതിശാസ്ത്രത്തിലെ ദൃഗ്ഭ്രംശകോണ്.
ഇനി താഴെയുള്ള ചിത്രം നോക്കൂ.
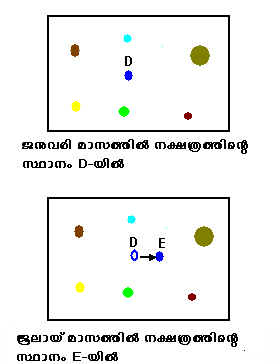
A എന്ന ബിന്ദു ഭൂമിയുടെ സൂര്യനു ചുറ്റുമുള്ള പാതയിലെ ജനുവരി മാസത്തെ സ്ഥാനം സൂചിപ്പിക്കുന്നു. Bഎന്ന ബിന്ദു ജൂലായ് മാസത്തെ ഭൂമിയുടെ സ്ഥാനത്തേയും സൂചിപ്പിക്കുന്നു. ഈ രണ്ട് ബിന്ദുക്കളില് നിന്ന് ആറ് മാസത്തെ ഇടവേളയില് C എന്ന സമീപ നക്ഷത്രത്തെ നിരീക്ഷിക്കുന്നു എന്നിരിക്കട്ടെ. പശ്ചാത്തല നക്ഷത്രങ്ങള് എന്നു കാണിച്ചിരിക്കുന്ന നക്ഷത്രങ്ങള് C എന്ന നക്ഷത്രത്തില് നിന്ന് വളരെയധികം ദൂരത്തുള്ളവ ആണ്. A എന്ന ബിന്ദുവില് നിന്ന് C യെ നിരീക്ഷിക്കുമ്പോള് അതിനെ D എന്ന ഭാഗത്തുള്ള പശ്ചാത്തല നക്ഷത്രങ്ങളോടൊപ്പം കാണുന്നു. B എന്ന ബിന്ദുവില് നിന്ന് നിരീക്ഷിക്കുമ്പോള് E എന്ന ഭാഗത്തുള്ള പശ്ചാത്തല നക്ഷത്രങ്ങളോടൊപ്പവും. ഇങ്ങനെ ഭൂമിയുടെ സ്ഥാനം മാറുന്നതിനനുസരിച്ച് (അതായത് നിരീക്ഷകന്റെ സ്ഥാനം) ഒരു സമീപ നക്ഷത്രത്തിന്റെ സ്ഥാനത്തിനു വരുന്ന ആപേക്ഷികമായ മാറ്റത്തെയാണ് നക്ഷത്ര ദൃഗ്ഭ്രംശം (Stellar parallax) എന്നു പറയുന്നത്. C എന്ന നക്ഷത്രം ഭൂമിയുടെ രണ്ട് സ്ഥാനത്തിനും മേല് ചെലുത്തുന്ന കോണീയ അളവിനെ parallax angle (ദൃഗ്ഭ്രംശം കോണ്) എന്നു പറയുന്നു. മുകളില് വിവരിച്ചതിന്റെ ഒരു ഫോട്ടോ എടുക്കുക ആണെങ്കില് അത് ഏകദേശം താഴെ കാണുന്ന മാതിരി ഇരിക്കും. (ഈ ചിത്രം കുറച്ച് exaggrate ചെയ്ത് വരച്ചാണ്. ശരിക്കും ഇത്ര മാറ്റം വരില്ല).
ജനുവരി മാസത്തില് കാണുന്ന D എന്ന ഭാഗത്തു നിന്ന് നമ്മള് നിരീക്ഷിക്കുന്ന നക്ഷത്രം ജൂലായ് മാസത്തില് Eഎന്ന ഭാഗത്തേക്ക് മാറിയിക്കുന്നു. ഈ മാറ്റം എത്രയാണോ അതാണ് പാരലാക്സ് കോണ്.
നക്ഷത്രത്തിലേത്തിലേക്കുള്ള ദൂരം കൂടുംതോറും ദൃഗ്ഭ്രംശകോണ് കുറഞ്ഞു വരും. താഴെയുള്ള ചിത്രങ്ങള് ശ്രദ്ധിക്കൂ.
ഒന്നാമത്തെ ചിത്രത്തില് നക്ഷത്രം അടുത്തായതു കൊണ്ട് ദിഗ്ഭ്രംശകോണ് കൂടുതല് ആണെന്ന് കാണാം. രണ്ടാമത്തെ ചിത്രത്തില് നക്ഷത്രം കുറച്ചുകൂടി അകലെയായതുകൊണ്ട് ദൃഗ്ഭ്രംശകോണ് കുറവാണെന്ന് കാണാം. അതായത് നക്ഷത്രത്തിലേക്കുള്ള ദൂരം കൂടും തോറും ദൃഗ്ഭ്രംശ കോണ് കുറഞ്ഞു വരുന്നു. മറ്റൊരു വിധത്തില് പറഞ്ഞാല് നമ്മുടെ സമീപത്തുള്ള നക്ഷത്രങ്ങളുടെ ദൃഗ്ഭ്രംശകോണ് അളക്കാനും അതു വഴി നക്ഷത്രത്തിലേക്കുള്ള ദൂരവും കാണാന് ഈ പ്രതിഭാസം കൊണ്ട് കഴിയൂ.
നക്ഷത്രങ്ങള് വളരെയധികം അകലെയായത് കൊണ്ട് അവ ഉണ്ടാക്കുന്ന ദൃഗ്ഭ്രംശകോണും വളരെ ചെറുതായിരിക്കും. നഗ്ന നേത്രം കൊണ്ട് നമുക്ക് ദൃഗ്ഭ്രംശകോണ് അളക്കാനേ പറ്റില്ല. അതുകൊണ്ടാണ് നമ്മുടെ പൂര്വ്വികര്ക്ക് ദൃഗ്ഭ്രംശം എന്ന ഈ പ്രതിഭാസം അറിയാമായിരുന്നിട്ടും നക്ഷത്രങ്ങളിലേക്കുള്ള ദൂരം ഇത് ഉപയോഗിച്ച് നിര്ണ്ണയിക്കാന് കഴിയാതെ പോയത്. പക്ഷെ ശക്തിയേറിയ ദൂരദര്ശിനിയുടെ സഹായത്തോടെ നമ്മള്ക്ക് ദൃഗ്ഭ്രംശ കോണ് കൃത്യതയോടെ അളക്കാം.
നക്ഷത്ര ദൃഗ്ഭ്രംശ സമവാക്യം
നമ്മള് ജ്യോതിശാസ്ത്രത്തിലെ ഏകകങ്ങള് എന്ന പോസ്റ്റില് നിന്ന് ഭൂമിയില് നിന്ന് സൂര്യനിലേക്കുള്ള ദൂരം 1 AU (ഒരു സൌരദൂരം) ആണെന്ന് മനസ്സിലാക്കി.
6 മാസത്തെ ഇടവേളയില് രണ്ട് നിരീക്ഷണ സ്ഥാനങ്ങള് തമ്മിലുള്ള ദൂരം 2 AU ആയിരിക്കും. ഇങ്ങനെ രണ്ട് സ്ഥാനത്ത് നിന്ന് അളന്നപ്പോള് നമുക്ക് കിട്ടിയ പാരലാക്സ് കോണ് 2p എന്നിരിക്കട്ടെ. ഇനി നമ്മള്ക്ക് നക്ഷത്രത്തിലേക്കുള്ള ദൂരം d = 1/p എന്ന സമവാക്യം ഉപയോഗിച്ചു (ഈ സമവാക്യത്തിന്റെ derivation അറിയാന് (derivation-ന്റെ മലയാളം ആരെങ്കിലും പറഞ്ഞു തരൂ) താഴെയുള്ള അനുബന്ധം നോക്കൂ.) കണ്ടു പിടിക്കാന് പറ്റും. ഇവിടെ ദൃഗ്ഭ്രംശ കോണ് p എന്നത് ആര്ക്ക് സെക്കന്റ് ഏകകത്തില് ആയിരിക്കണം. ഈ സമവാക്യം നിര്ദ്ധാരണം ചെയ്താല് നമുക്ക് കിട്ടുന്ന ദൂരത്തിന്റെ ഏകകം പാര്സെക്കില് ആയിരിക്കും. അതായത് ഒരു നക്ഷത്രത്തിന്റെ ദിഗ്ഭ്രംശ കോണ് ആര്ക്ക് സെക്കന്റ് കണക്കില് അറിയാമെങ്കില് അതിന്റെ inverse (ഇതിന്റെ മലയാളം എന്താണാവോ?) കണ്ടാല് നക്ഷത്രത്തിലേക്കുള്ള ദൂരം പാര്സെക്ക് കണക്കില് കിട്ടും. ഇതുകൊണ്ടാണ് പാര്സെക് എന്ന ഏകകത്തിന് ജ്യോതിശാസ്ത്രത്തില് വളരെ പ്രാധാന്യം ഉണ്ടെന്ന് മുന്പുള്ള പോസ്റ്റുകളില് പറഞ്ഞത്.
ആദ്യമായി പാരലാക്സ് കോണ് അളന്നത് 61 Cygni എന്ന നക്ഷത്രത്തിനാണ്. (61 Cygni എന്ന പേര് വന്നത് എങ്ങനെയാണ് എന്ന് ഇനി പറഞ്ഞു തരേണ്ടല്ലോ. അറിയാത്തവര് നക്ഷത്രങ്ങളെ നാമകരണം ചെയ്യുന്നത് എങ്ങനെ എന്ന പോസ്റ്റ് വായിക്കുക.) 1838-ല് Friedrich Bessel എന്ന ജ്യോതിശാസ്ത്രജ്ഞനാണ് ഈ നക്ഷത്രത്തിന്റെ പാരലാക്സ് കോണ് അളന്നത്. അദ്ദേഹത്തിന് കിട്ടിയ മൂല്യം 0.30 ആര്ക്ക് സെക്കന്റ് എന്നാണ്.അതിന്റെ അര്ഥം അത് 1/p=1/0.30 = 3.3 പാര്സെക് ദൂരത്താണ് എന്നാണല്ലോ.
പാരലാക്സ് ഉപയോഗിച്ച് നമ്മളോട് അടുത്ത നക്ഷത്രങ്ങളിലേക്കുള്ള ദൂരം മാത്രമേ അളക്കാന് പറ്റുകയുള്ളൂ. കാരണം നമ്മളോട് അടുത്ത നക്ഷത്രങ്ങളുടെ പാരലാക്സ് കോണ് തന്നെ വളരെ ചെറുതാണ്. നമ്മളോട് ഏറ്റവും അടുത്ത നക്ഷത്രമായ പ്രോക്സിമ സെന്റോറിക്കാണ് ഏറ്റവും അധികം പാരലാക്സ് കോണ് ഉള്ളത്. പക്ഷെ അത് തന്നെ 0.772 ആര്ക്ക് സെക്കന്റ് മാത്രമേ ഉള്ളൂ.
പ്രോക്സിമ സെന്റോറിയുടെ പാരലാക്സ് കോണ് 0.772 ആര്ക്ക് സെക്കന്റ് ആണെന്ന് തന്നിട്ടുണ്ടല്ലോ. ആ നക്ഷത്രത്തിലേക്കുള്ള ദൂരം എത്രയാണെന്ന് പാര്സെക്കിലും, AU കണക്കിലും, പ്രകാശ വര്ഷത്തിലും, കിലോമീറ്ററിലും കണ്ടുപിടിച്ച് കമെന്റ് ആയി ഇടൂ. സഹായത്തിനു ജ്യോതിശാസ്ത്രത്തിലെ ഏകകങ്ങള് എന്ന പോസ്റ്റും ഈ പോസ്റ്റും ഉപയോഗിക്കാം.
ഏറ്റവും അടുത്ത നക്ഷത്രമായ പ്രോക്സിമ സെന്റോറിയുടെ പാരലാക്സ് കോണ് തന്നെ ഇത്രയും ചെറുതാണെങ്കില് പിന്നേയും അകലെ കിടക്കുന്ന നക്ഷത്രങ്ങളുടെ പാരലാക്സ് കോണ് എത്ര ചെറുതായിരിക്കും എന്ന് ഊഹിക്കാമല്ലോ. മാത്രമല്ല ദൂരം കൂടും തോറും നമുക്ക് പാരലാക്സ് കോണിന്റെ കൃത്യതയും കുറഞ്ഞു വരും. അതിനാല് പാരലാക്സ് ഉപയോഗിച്ചുള്ള ദൂര നിര്ണ്ണയം സമീപ നക്ഷത്രങ്ങള്ക്ക് മാത്രമേ ഉപയോഗിക്കാറുള്ളൂ.കഴിഞ്ഞ പോസ്റ്റില് നമ്മള് ഹിപ്പാര്ക്കസ് കാറ്റലോഗിനെ പരിചയപ്പെട്ടുവല്ലോ. ആ പോസ്റ്റില് പറഞ്ഞിരുന്നത് പോലെ Hipparcos (High precision parallax collecting satellite) എന്ന കൃത്രിമ ഉപഗ്രഹം ഉപയോഗിച്ച് ശാസ്ത്രജ്ഞര് 1,18,000 ത്തോളം സമീപ നക്ഷത്രങ്ങളുടെ പാരലാക്സ് കോണ് അതീവ കൃത്യതയോടെ അളന്നു. ബഹിരാകാശത്ത് നിന്ന് അളന്നതിനാല് ഹിപ്പാര്ക്കസിന് ഭൌമ ദൂരദര്ശിനികളേക്കാള് കൃത്യതോടെ പാരലാക്സ് കോണ് അളക്കാന് പറ്റി. എന്നിട്ട് അതിനെ അടിസ്ഥാനമാക്കി ഒരു കാറ്റലോഗ് ഉണ്ടാക്കി അതാണ് ഹിപ്പാര്ക്കസ് കാറ്റലോഗ് എന്ന് നമ്മള് കഴിഞ്ഞ പോസ്റ്റില് പരിചയപ്പെട്ടുവല്ലോ. ഈ കാറ്റലോഗ് പ്രകാരം പ്രോക്സിമ സെന്റോറിയുടെ പേര് HP 70890 എന്നാണ്.
അനുബന്ധം
ദൃഗ്ഭ്രംശ കോണ് ഉപയോഗിച്ച് നക്ഷത്രങ്ങളിലേക്കുള്ള ദൂരം കാണുന്ന സമവാക്യമായ d = 1/p എങ്ങനെയാണ് derive ചെയ്യുന്നത് എന്ന് ഇവിടെ കാണിച്ചിരിക്കുന്നു.
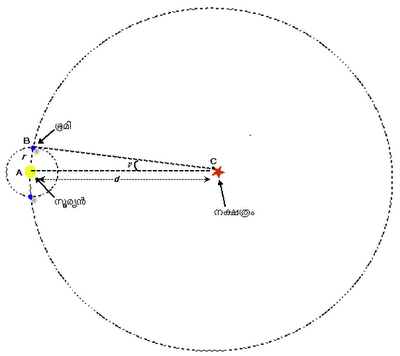
നക്ഷത്രത്തിലേക്കുള്ള ദൂരം d-യും, സൂര്യനില് നിന്ന് ഭൂമിയിലേക്കുള്ള ദൂരം r-ഉം നക്ഷത്രം ഉണ്ടാക്കുന്ന പാരലാക്സ് p-യും എന്നിരിക്കട്ടെ. ഇനി നിങ്ങള് നിരീക്ഷിക്കുന്ന നക്ഷത്രത്തെ കേന്ദ്രമാക്കി ഒരു സാങ്കല്പിക വൃത്തം സങ്കല്പ്പിക്കുക. താഴെയുള്ള ചിത്രം നോക്കൂ.
(ഇനി താഴോട്ടുള്ളത് ചിത്രം ആയിട്ടാണ് കൊടുത്തിരിക്കുന്നത്. ഈ mathematical expressions എങ്ങനെ html-ല്എഴുതും എന്ന് എനിക്കറിയില്ല. അറിയുന്നവര് ദയവായി അത് കമെന്റ് ആയി ഇടുകയോ മെയില് അയക്കുകയോ ചെയ്ത് സഹായിക്കുക.)
അതായത് ഒരു നക്ഷത്രത്തിന്റെ ദിഗ്ഭ്രംശ കോണ് ആര്ക്ക് സെക്കന്റ് കണക്കില് അറിയാമെങ്കില് അതിന്റെ inverse കണ്ടാല് നക്ഷത്രത്തിലേക്കുള്ള ദൂരം പാര്സെക്ക് കണക്കില് കിട്ടും.
ഈ സമവാക്യത്തിന്റെ ഏറ്റവും ലളിതമായ ഒരു derivation ആണ് ഇവിടെ കൊടുത്തത്. മറ്റു പല വിധത്തിലും ഈ സമവാക്യത്തില് എത്തിചേരാം.
കുറിപ്പ്:
d = (206265AU)/p എന്ന സമവാക്യത്തിനേയും 206265 AU = 1 pc എന്നു സങ്കല്പിച്ചതിന്റേയും ഭൌതീക അര്ത്ഥം വളരെ ലളിതമാണ്. അത് ഇംഗ്ലീഷില് തന്നെ കൊടുക്കുന്നു. മലയാളീകരിച്ചാല് പൂര്ണ്ണ അര്ത്ഥം കിട്ടില്ല.
An object at a distance of 206,265 AU will subtend an angle of one parallax second of arc. parallax second ഇതില് നിന്നാണ് parsec എന്ന വാക്ക് ഉണ്ടായത്.






5 comments:
നന്നായിട്ടൂണ്ട് ഷിജു!
വളരെ വിജ്ഞാനപ്രദമാണ് ഷിജുവിന്റെ ഓരോ പോസ്റ്റും. എല്ലാം വായിച്ചിട്ട് പ്രിന്റെടുത്ത് സൂക്ഷിക്കുന്നുണ്ട്.
Post is very good shiju. I ve calculated the distances.. and it is the same as u told in one of the previous post.
ഷിജു, കുറേ നാളായി പോസ്റ്റ് ഒന്നും കാണാനില്ലല്ലോ?
ഷിജുജീ,
താങ്കളുടെ ബ്ലോഗ് ഞാന് ബുക്മാര്ക്കു ചെയ്തു സൂക്ഷിക്കുന്നു, എന്നും ആകാശവും നക്ഷത്രങ്ങളും അത്ഭുതം തന്നെ.”ഈ വല്ലിയില് നിന്നു ചെമ്മേ പൂക്കള് പോകിന്നതാ പറന്നമ്മെ.”ചിത്രശലഭങ്ങളെ തെറ്റിധരിച്ച ആ ഉണ്ണിയെപ്പോലെ, ആകാശം ഇന്നും ആ വരിയില് തന്നെ.താങ്കളുടെ ബ്ലോഗിലൂടെ ആ അമ്മ പറഞ്ഞു തന്നതു പോലെ, “തെറ്റി നിനക്കുണ്ണി ചൊല്ലാം” എന്നുള്ള ഉത്തരങ്ങള് മനസ്സിലാക്കാന് ശ്രമിക്കുന്നു.ഈ അറിവിന്റെ മുത്തുകള്ക്കു് എന്റെ ഭാവുകങ്ങള്.
ഷിജു, കുറച്ചു ദിവസമേ ആയിട്ടുള്ളൂ ഈ ബ്ലോഗ് കണ്ടിട്ട്. എന്നാലും ഈ ബ്ലോഗില് തന്നെ കുത്തിയിരുന്ന് വായന ആണു പ്രധാന ടൈം പാസ്. ഇത്ര ലളിതമായി ഈ വക വിഷയങ്ങള് പണ്ടേ ആരെങ്കിലും പറഞ്ഞു തന്നിരുന്നെങ്കില് ഞാന് ആരൊക്കെയോ ആയിപ്പോയേനെ. എന്നാലും താങ്കളുടെയും ഉമേഷേട്ടന്റെയും ബ്ലോഗുകളില് നിന്നും കഴിഞ്ഞ രണ്ടു മാസമായി കിട്ടിയ അറിവില് എനിക്ക് തെല്ല് അഹങ്കാരം ഉണ്ടായിട്ടുണ്ടോ എന്ന ഒരു ഭയം ഇല്ലാതില്ല.
പിന്നെ മുകളില് ചോദിച്ച ചോദ്യത്തിന് ഇതുവരെ ആരും ഉത്തരം അയക്കഞ്ഞതുകൊണ്ട് എഴുതുന്നു:
Distance to Proxima Centauri = 1/0.772 = 1.295 parsec
അതായത്,
1.295 x 3.26 light years = 4.22 light years
അല്ലെങ്കില്
1.295 x 206265 AU = 267182.642 AU
അഥവാ,
1.295 x 30.857 x 10^12 KM = 4x10^13 KM (ഏകദേശം)
ശരിയാണോ എന്തോ?
എന്തായാലും ബാക്കിയുള്ള പോസ്റ്റുകള് കൂടി വായിച്ചു തീര്ക്കട്ടെ. വളരെ interesting ആകുന്നുണ്ട്.
ഒരുപാടു നന്ദി.
Post a Comment