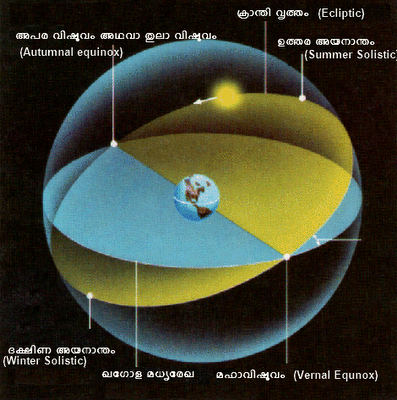
1. കോണീയ അളവ് (Angular measure)
ജ്യോതിര്ഗോളങ്ങളുടെ സ്ഥാനവും ഭൂമിയില് നിന്ന് നോക്കുമ്പോള് അവയുടെ വലിപ്പവും മറ്റും സൂചിപ്പിക്കുവാനും ജ്യോതിശ്ശാസ്ത്രജ്ഞര്ക്ക് ഏറ്റവും അധികം ഉപയോഗിക്കേണ്ടി വരുന്ന ഒരു ഏകകം ആണ് കോണീയ അളവ് (Angular measure). ഇത് നമ്മള്ക്കെല്ലാം പരിചയം ഉള്ളതും നമ്മള് ചെറിയ ക്ലാസ്സ് തൊട്ടേ പഠിക്കുന്നതും ആണ്. കോണിനെ ഏറ്റവും ലളിതമായി ഒരു common ബിന്ദുവില് കൂട്ടിമുട്ടുന്ന രണ്ട് രേഖകളുടെ ഇടയിലുള്ള ആളവ് എന്ന് നിര്വചിക്കാം.

ചന്ദ്രന്റെ കോണീയ അളവ്
ജ്യോതിശാസ്ത്രജ്ഞര് ചന്ദ്രന്റേയും സൂര്യന്റേയും കോണീയ അളവ് 0.5° ആണെന്ന് പറയും. ചന്ദ്രന്റെ കോണീയ അളവ് തന്നെ അര ഡിഗ്രി ആണെങ്കില് അതിലും എത്രയോ ചെറിയ വസ്തുക്കളെ സൂചിപ്പിക്കാന് ഡിഗ്രി മതിയാകില്ല. അതിനാല് ഡിഗ്രിയെ പിന്നേയും ചെറുതായി വിഭജിച്ച് ആര്ക്ക് മിനിറ്റും ആര്ക്ക് സെക്കന്റും ഉപയോഗിക്കേണ്ടി വരുന്നു. ഒരു ഡിഗ്രിയെ 60 ഭാഗമായി തിരിക്കുമ്പോള് ലഭിക്കുന്ന ഒരു ഭാഗത്തിന് ഒരു ആര്ക് മിനിറ്റ് എന്ന് പറയുന്നു. ഈ ഒരു മിനിറ്റിനെ 60 ഭാഗമായി ഭാഗിക്കുമ്പോള് ലഭിക്കുന്ന ഒരു ഭാഗത്തിന് ഒരു ആര്ക് സെക്കന്റ് എന്ന് പറയുന്നു. ആര്ക് മിനിറ്റിനെ ‘ എന്ന ചിഹ്നം കൊണ്ടും ആര്ക് സെക്കനന്റിനെ ‘‘ എന്ന ചിഹ്നം കൊണ്ടും സൂചിപ്പിക്കുന്നു.
1°=60 ആര്ക് മിനിറ്റ് = 60‘
1‘=60 ആര്ക് സെക്കന്റ് = 60‘‘
1°=60‘=3600‘‘
ഉദാഹരണത്തിന് ശനി ഗ്രഹത്തെ ഭൂമിയില് നിന്ന് നോക്കുമ്പോള് ഉള്ള കോണീയ അളവ് 17.9 ‘’. അതില് നിന്ന് അത് എത്രയും ചെറുതാണെന്ന് ഊഹിക്കാമല്ലോ.
ii. റേഡിയന് (radian)
കോണീയ അളവിന്റെ മറ്റൊരു പ്രധാന ഏകകം ആണ് radian (റേഡിയന്). ഡിഗ്രിയുടെ കണക്കില് നമ്മള് ഒരു വൃത്തത്തില് 360 ഡിഗ്രി ഉണ്ടെന്ന് പറയും. എന്നാല് റേഡിയന് കണക്കില് ഒരു വൃത്തത്തില് 2π റേഡിയന് ഉണ്ടെന്ന് പറയും.
അതായത്,
2π rad = 360°
π rad = 180°
1 rad = (180/π)°
= (180* 60* 60/π) ആര്ക്ക് സെകന്റ് = 206265 ‘’
1 rad = 206265 ‘’
അതായത് ഒരു റേഡിയനില് 206265 ‘’ ഉണ്ടെന്ന് നമുക്ക് കിട്ടുന്നു.
ഇതു വളരെ പ്രാധാന്യം ഉള്ള ഒരു ഉത്തരം ആണ്. പാര്സെക് എന്ന ഏകകത്തെ കുറിച്ചു പഠിക്കുമ്പോഴും പാരലാക്സിനെ കുറിച്ച് പഠിക്കുമ്പോഴും ഇതിനു വളരെ പ്രാധാന്യം ഉണ്ട്. കൂടുതല് വിവരം പാരലാക്സിനെ കുറിച്ചുള്ള പോസ്റ്റില്.
2. ദൂരം/നീളം/വലിപ്പം (Length/Distance)
അടുത്തത് ദൂരത്തെ സൂച്ച്പ്പിക്കുവാന് ജ്യോതിശാസ്ത്രജ്ഞര് ഉപയോഗിക്കുന്ന ഏകകങ്ങള് ഏതൊക്കെ ആണെന്ന് നോക്കാംനമ്മള് സാധാരണ ഭൂമിയെ ആവശ്യത്തിന് ദൂരം അല്ലെങ്കില് വലിപ്പത്തെ സൂചിപ്പിക്കാന് മീറ്ററും കിലോമീറ്ററും ഒക്കെ ആണ് ഉപയോഗിക്കുന്നത്.
പക്ഷെ ബഹിരാകാശത്തെ ദൂരം സൂചിപ്പിക്കാന് ഈ ഏകകം അപര്യാപ്തമാണ്. കാരണം ഭൂമിയോട് ഏറ്റവും അടുത്തു കിടക്കുന്ന ഖഗോള വസ്തുവായ ചന്ദ്രനിലേക്കുള്ള ദൂരം തന്നെ 3,84,403 കിലോമീറ്റരാണ്. അപ്പോള് മറ്റ് ഗ്രഹങ്ങളിലേക്കും, സൂര്യനിലേക്കും, നക്ഷത്രങ്ങളിലേക്കുമൊക്കെയുള്ള ദൂരം കിലോമീറ്ററില് സൂചിപ്പിക്കാന് തുടങ്ങിയാല് ആ സംഖ്യ മനുഷ്യന് സങ്കല്പ്പിക്കാവുന്നതിലും വലുതായിരിക്കുമെന്ന് മനസ്സിലാക്കാമല്ലോ. അതിനാല് ജ്യോതിശാസ്ത്രജ്ഞര്ക്ക് ദൂരത്തെ സൂചിപ്പിക്കാന് മറ്റ് ഏകകങ്ങള് കണ്ടെത്തേണ്ടി വന്നു. അവ താഴെ പറയുന്നു.
i. അസ്ട്രോണൊമിക്കല് യൂണിറ്റ് (AU)
ഇത് സൌരയൂഥത്തിലെ ഗ്രഹങ്ങളും സൂര്യനും മറ്റ് വസ്തുക്കള് തമ്മിലുള്ള ദൂരം സൂചിപ്പിക്കാനാണ് ഉപയോഗിക്കുന്നത്. ലളിതമായി പറഞ്ഞാല് സൂര്യനും ഭൂമിയും തമ്മിലുള്ള ദൂരം എത്രയാണോ അതാണ് ഒരു അസ്ട്രോണൊമിക്കല് യൂണിറ്റ് .
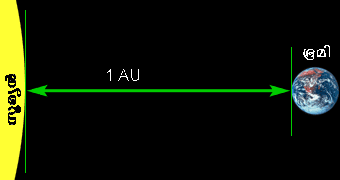 ഒരു അസ്ട്രോണൊമിക്കല് യൂണിറ്റ്
ഒരു അസ്ട്രോണൊമിക്കല് യൂണിറ്റ്
ഇത് വളരെ കൃത്യമായി പറഞ്ഞാല് 149,597,870 കിലോമീറ്ററാണ് . സൂര്യനില് നിന്ന് ഭൂമിയിലേക്ക് പതിനാല് കോടി തൊണ്ണൂറ്റി അഞ്ച് ലക്ഷത്തി തൊണ്ണൂറ്റി ഏഴായിരത്തി എണ്ണൂറ്റി എഴുപത് കിളൊമീറ്ററാണ് എന്ന് പറയുന്നതാണോ ഒരു അസ്ട്രോണൊമിക്കല് യൂണിറ്റ് ആണ് എന്ന് പറയുന്നതാണോ എളുപ്പം. സൂര്യനില് നിന്ന് ഭൂമിയിലേക്ക് ഇത്ര ദൂരം ആണെങ്കില് മറ്റ് ഗ്രഹങ്ങളിലേക്ക് എത്ര വലിയ സഖ്യയായിരിക്കും എന്ന് ഊഹിക്കാമല്ലോ. അപ്പോള് എന്ത് കൊണ്ടാണ് ഇങ്ങനെ ഒരു ഏകകം ജ്യോതിശാസ്ത്രജ്ഞര് ഉപയോഗിക്കാന് തുടങ്ങിയത് എന്ന് മനസ്സിലാക്കാമല്ലോ.
ഈ ഏകക പ്രകാരം സൂര്യനില് നിന്ന്
ചൊവ്വയിലേക്ക് - 1.52 AU
വ്യാഴത്തിലേക്ക് -5.2 AU
പ്ലൂട്ടോയിലേക്ക് - 39.5 AU
ഇങ്ങനെയാണ് വിവിധ ഗ്രഹങ്ങളിലേക്കുള്ള ദൂരം.
ജുപിറ്ററിനെയും മറ്റ് ഗ്രഹങ്ങളേയും പഠിക്കാന് മനുഷ്യന് വിക്ഷേപിച്ച വോയേജര് 1 എന്ന ബഹിരാകാശ വാഹനം ഇപ്പോള് സൂര്യനില് നിന്ന് 100 AU ദൂരത്താണെന്ന് പറയപ്പെടുന്നു. വിവിധ ഗ്രഹങ്ങളിലേക്ക് സൂര്യനില് നിന്ന് AU ഏകകത്തില് ഉള്ള ദൂരം താഴെയുള്ള പട്ടികയില് കൊടുത്തിരിക്കുന്നു.
| ഗ്രഹം | സൂര്യനില് നിന്ന് ഗ്രഹത്തിലേക്ക് AU ഏകകത്തില് ഉള്ള ദൂരം |
| ബുധന് | 0.3871 |
| ശുക്രന് | 0.7233 |
| ഭൂമി | 1.000 |
| ചൊവ്വ | 1.5236 |
| വ്യാഴം | 5.2028 |
| ശനി | 9.5387 |
| യുറാനസ് | 19.1913 |
| നെപ്റ്റ്യൂണ് | 30.0610 |
അപ്പോള് സൌരയൂഥത്തിലെ വസ്തുക്കള് തമ്മിലുള്ള അകലം സൂചിപ്പിക്കാന് AU മതി. ഇനി ഇപ്പോള് സൌരയൂഥം വിട്ട് പുറത്തേക്ക് നക്ഷത്രങ്ങളിലേക്കുള്ള ദൂരം ഒക്കെ പറയുമ്പോഴോ.
ഉദാഹരണത്തിന് സൂര്യന് കഴിഞ്ഞാല് നമ്മളോട് ഏറ്റവും അടുത്ത നക്ഷത്രമായ പ്രോക്സിമാ സെന്ടോറിയിലേക്ക് AU ന്റെ കണക്കില് തന്നെ പറഞ്ഞാല് 2, 68,000 AU ആണ് ദൂരം. അപ്പോള് അതിനും അപ്പുറം കിടക്കുന്ന നക്ഷത്രങ്ങളിലേക്കും ഗാലക്സികളിലേക്കും മറ്റുമുള്ള ദൂരം AU ല് സൂചിപ്പിച്ചാല് നമുക്ക് സങ്കല്പ്പിക്കാന് പറ്റാത്ത അത്രയും വലിയ സംഖ്യയാകും.അതു കൊണ്ട് ജ്യോതിശാസ്ത്രജ്ഞര്ക്ക് വേറൊരു ഏകകം കൂടി ഉപയോഗിക്കേണ്ടി വന്നു. അതാണ് അടുത്തത്.
ii. പ്രകാശ വര്ഷം (Light year)
പ്രകാശം ഒരു സെക്കന്റില് 3 ലക്ഷം കിലോമിറ്റര് സഞ്ചരിക്കും എന്ന് നിങ്ങള് കേട്ടിട്ടുണ്ടാവുമല്ലോ. ഈ കണക്കില് ഒരു മിനിറ്റ് കൊണ്ട് തന്നെ ഏകദേശം ഒരു കോടി എണ്പത് ലക്ഷം കിലോമീറ്റര് സഞ്ചരിക്കും. അപ്പോള് ഒരു വര്ഷത്തിലോ. പ്രകാശം ഒരു വര്ഷം കൊണ്ട് ഏകദേശം 95,000 കോടി കിലോമീറ്റര് സഞ്ചരിക്കും. അപ്പോള് ഇതിനെ ഒരു ഏകകം ആക്കിയാല് നക്ഷത്രങ്ങളിലേക്കൊക്കെയുള്ള ദൂരം സൂചിപ്പിക്കാന് നല്ലൊരു ഏകകം ആയി. അതാണ് ജ്യോതിശാസ്ത്രജ്ഞന്മാര് ചെയ്തത്.
ഈ ഏകകം അനുസരിച്ച് നമ്മളോട് ഏറ്റവും അടുത്ത നക്ഷത്രമായ പ്രോക്സിമാ സെന്ടോറിയിലേക്ക് ഉള്ള ദൂരം 4.2 പ്രകാശ വര്ഷമാണ്. ഈ ഏകകത്തിന്റെ വേറൊരു മെച്ചം ഒരു നക്ഷത്രത്തിലേക്കോ ഗാലക്സികളിലേക്കോ ഉള്ള അകലം പ്രകാശ വര്ഷ ഏകകത്തില് അറിഞ്ഞാല് നമ്മള് അത്രയും വര്ഷം പുറകിലേക്കാണ് നോക്കുന്നത് എന്നര്ത്ഥം.
ഉദാഹരണത്തിന് പ്രോക്സിമാ സെന്ടോറിയിലേക്ക് ഉള്ള ദൂരം 4.2 പ്രകാശ വര്ഷമാണ് എന്ന് പറഞ്ഞാല് ആ നക്ഷത്രത്തില് നിന്ന് 4.2 വര്ഷം മുന്പ് പുറപ്പെട്ട പ്രകാശം ആണ് നമ്മള് ഇപ്പോള് കാണുന്നത് എന്ന് അര്ത്ഥം. അതായത് 4.2 വര്ഷം മുന്പുള്ള പ്രോക്സിമാ സെന്ടോറിയെ ആണ് നമ്മള് ഇന്ന് കാണുന്നത് . അപ്പോള് നമ്മള് ഇന്ന് ഭൂമിയില് നിന്ന് നിരീക്ഷിക്കുമ്പോള് കാണുന്ന നക്ഷത്രങ്ങളുടേയും ഗ്ഗാലക്സ്സികളുമൊക്കെ എത്രയും പ്രകാശ വര്ഷം അകലെയാണോ അത്രയും വര്ഷം മുന്പുള്ള നക്ഷത്രങ്ങളുടേയും ഗ്ഗാലക്സ്സികളുമൊക്കെ ആണ് നമ്മള് കാണുന്നത് എന്ന് സാരം.
iii. പാര്സെക് (Parsec)
പ്രകാശ വര്ഷം കൂടാതെ വേറൊരു ഏകകം കൂടി നക്ഷത്രങ്ങളിലേക്കും ഗാലക്സികളിലേക്കും ഒക്കെ ഉള്ള ദൂരം കണക്ക് കൂട്ടാന് ഉപയോഗിക്കുന്നുണ്ട്. അതിന്റെ പേരാണ് പാര്സെക്. ഇത് പ്രകാശ വര്ഷത്തിലും വലിയ ഏകകം ആണ്. ആദ്യം പാര്സെക് എന്താണെന്ന് വിശദീകരിക്കാം. താഴെയുള്ള ചിത്രം ശ്രദ്ധിക്കൂ.
 ഒരു പാര്സെക്
ഒരു പാര്സെക്ചിത്രത്തില് കാണിച്ചിരിക്കുന്ന പ്രകാരം സൂര്യനും ഭൂമിയും തമ്മിലുള്ള അകലം 1 AU ആണെന്ന് നമ്മള് മുകളിലെ വിശദീകരണത്തില് നിന്ന് മനസ്സിലാക്കി. ഈ 1 AU ദൂരം, ഒരു ആര്ക്ക് സെക്കന്റ് കോണീയ ആളവ് എത്രയും ദൂരത്താണോ ചെലുത്തുന്നത് അതിനെയാണ് ഒരു പാര്സെക് എന്ന് പറയുന്നത് . (One parsec is the distance at with 1 AU subtends an angle of one arc second). ഇത് വളരെ കൃത്യമായി പറഞ്ഞാല് 30.857×1012 കിലോമീറ്റര് ആണ്. എന്തൊരു വലിയ സംഖ്യ അല്ലേ. ഇത്രയും കിലോമീറ്ററിനെ പ്രകാശവര്ഷത്തിലേക്ക് മാറ്റിയാല് 3.26 പ്രകാശ വര്ഷം ആണെന്ന് കിട്ടുന്നു. അതായത് ഒരു പാര് സെക് എന്ന് പറഞ്ഞാല് 3.26 പ്രകാശ വര്ഷം.
ഇത്രയും കിലോമീറ്ററിനെ AU ഏകകത്തിലേക്ക് മാറ്റിയാല് 206265 AU എന്നു കിട്ടുന്നു. അതായത് 206265 AU കൂടിയതാണ് ഒരു പാര്സെക്ക്. 1 rad = 206265 ‘’ എന്ന ഉത്തരത്തിന്റെ പ്രാധാന്യം ഇപ്പോള് മനസ്സിലാക്കുന്നുണ്ടോ. കൂടുതല് പാരലാക്സിനെ കുറിച്ചുള്ള പോസ്റ്റില്.
നമ്മളോട് ഏറ്റവും അടുത്ത നക്ഷത്രമായ പ്രോക്സിമാ സെന്ടോറിയിലേക്ക് ഉള്ള ദൂരം 1.29 പാര്സെക് ആണ്. നമ്മുടെ ഗാലക്സിയായ ആകാശ ഗംഗയുടെ മദ്ധ്യത്തിലേക്ക് 8000 പാര്സെക് ദൂരമുണ്ട്. നമ്മുടെ സ്വന്തം ഗാലക്സിയുടെ മദ്ധ്യത്തിലേക്ക് തന്നെ ഇത്രയും ദൂരമുണ്ടെങ്കില് മറ്റുള്ള ഗാലക്സികളിലേക്ക് എത്രയധികം ദൂരം ഉണ്ടാകും. അതിനെ ഒക്കെ സൂചില്പ്പിക്കാന് കിലോ പാര്സെകും (103 പാര്സെകും) മെഗാ പാര്സെകും (106 പാര്സെകും) ഒക്കെ ജ്യോതി ശാസ്ത്രജ്ഞര് ഉപയോഗിക്കുന്നു. ഉദാഹരണത്തിന് നമ്മുടെ തൊട്ടടുത്ത ഗാലക്സിയായ ആന്ഡ്രോമിഡ ഗാലക്സ്സിയിലേക്ക് 0.77 മെഗാ പാര്സെക് ദൂരമുണ്ട്. നമ്മുടെ പ്രപഞ്ചം എത്ര വലിയതാണ് അല്ലേ.
പാരലാക്സിനെ കുറിച്ച് പറയുമ്പോള് പാര്സെക്കിന്റെ ശരിയായ ഉപയോഗം മനസ്സിലാകും.
ദൂരെയുള്ള നക്ഷത്രങ്ങളിലേക്കും ഗാലക്സികളിലേക്കും ഉള്ള ദൂരം പറയുമ്പോള് പ്രകാശ വര്ഷവും പാര്സെകും ഉപയോഗിക്കാറുണ്ട്.
3. ദ്രവ്യമാനം (Mass)
അവസാനമായി ഈ പോസ്റ്റില് ജ്യോതി ശാസ്ത്രജ്ഞര് ദ്രവ്യമാനത്തെ സൂചിപ്പിക്കാന് ഉപയോഗിക്കുന്ന ഏകകം കൂടി പരിചയപ്പെടുത്തട്ടെ.നമ്മള് സാധാരണ ദ്രവ്യമാനത്തെ സൂചിപ്പിക്കാന് കിലോഗ്രാമും ടണ്ണും ഒക്കെ ആണ് ഉപയോഗിക്കുന്നത്. ജ്യോതിശാസ്ത്രജ്ഞരും ഒരു പരിധി വരെ കിലോഗ്രാമാണ് ഉപയോഗിക്കുന്നത്. ഉദാഹരണത്തിന് ഭൂമിയുടേയും ഗ്രഹങ്ങളുടേയും ഒക്കെ ദ്രവ്യമാനം പറയാന് കിലോഗ്രാമാണ് ഉപയോഗിക്കുന്നത്. ഭൂമിയുടെ ദ്രവ്യമാനം 5.9742×10^24 കിലോഗ്രാമാണ്. വ്യാഴത്തിന്റെ ദ്രവ്യമാനം 1.899×10^27 കിലോഗ്രാമാണ്. സൂര്യന്റേത് 1.988 435 × 10^30 കിലോഗ്രാമാണ്.
ഇങ്ങനെ വര്ഗ്ഗം ഇട്ട് എത്ര കിലോഗ്രം വരെ വേണമെങ്കിലും പറയാം. പക്ഷെ മനുഷ്യന് സംഖ്യ
വലുതാകുംതോറും അതിന്റെ വലിപ്പത്തെ കുറിച്ച് ഊഹിക്കാന് പ്രയാസമാകും. പക്ഷെ നമ്മളോട് വ്യാഴത്തിന് ഭൂമിയുടെ 317 ഇരട്ടി ദ്രവ്യമാനം ഉണ്ടെന്ന് പറഞ്ഞാല് നമുക്ക് വ്യാഴത്തിന്റെ ഭൂമിയെ അപേക്ഷിച്ചുള്ള ദ്രവ്യമാനം വലിപ്പവും ഊഹിക്കാന് പറ്റുന്നു.
അതേ പോലെ സൂര്യന്റെ ദ്രവ്യമാനം അടിസ്ഥാനമാക്കി ശാസ്ത്രജ്ഞന്മാര് പുതിയ ഒരു ഏകകം കൂടി നിര്വചിച്ചു. അതാണ് സൌര ദ്രവ്യമാനം. അതായത് സൂര്യന്റെ ദ്രവ്യമാനമായ 1.988 435 × 10^30കിലോഗ്രാമിനെ ഒരു ഏകകം ആയി കരുതി. അപ്പോള് നക്ഷത്രളുടേയും മറ്റും ദ്രവ്യമാനം സൂചിപ്പിക്കാന് പറ്റിയ നല്ലൊരു ഏകകം കിട്ടി. ഈ ഏകകത്തെ M๏ എന്ന ചിഹ്നം കൊണ്ടാണ് സൂചിപ്പിക്കുന്നത് (M എന്നെഴുതി അതിന്റെ അടിയില് നടുക്ക് ഒരു കുത്തുള്ള വൃത്തം ഇടുന്നു. ) . ഈ ഏകക പ്രകാരം പ്രോക്സിമാ സെന്ടോറിയുടെ ഭാരം 0.12 M๏ ആണ്. ധ്രുവ നക്ഷത്രത്തിന്റേത് 6 M๏ ആണ്. തിരുവാതിര നക്ഷത്രത്തിന്റെ ഭാരം 15 M๏ ആണെന്നും പറയപ്പെടുന്നു.
4. സമയം (Time)
സമയം എന്നത് കൊണ്ട് ജ്യോതിശാസ്ത്രത്തില് ഉദ്ദേശിക്കുന്നത് രണ്ട് സംഭവങ്ങള് തമ്മിലുള്ള ഇടവേളയെയാണ്. സമയം സൂചിപ്പിക്കാന് നമ്മള് നിത്യജീവിതത്തില് ഉപയോഗിക്കുന്ന സെക്കന്റും വര്ഷവും ഒക്കെ തന്നെയാണ് ജ്യോതിശാസ്ത്രജ്ഞന്മാരും ഉപയോഗിക്കുന്ന് . അപൂര്വ്വമായി മിനിറ്റും മണിക്കൂറും ഉപയോഗിക്കാറുണ്ട്. ഉദാഹരണത്തിന് പ്രപഞ്ചത്തിന്റെ പ്രായം പറയുമ്പോള് ഏതാണ്ട് 1300 കോടി വര്ഷം ആയെന്ന് പറയും. പക്ഷെ സൂര്യന്റെ പ്രകാശം ഭൂമിയില് എത്താന് എട്ട് മിനിറ്റ് എടുക്കും എന്ന് പറയും. പക്ഷെ പ്രപഞ്ചം ഉണ്ടായി 10^-4 സെക്കന്റ് ആയപ്പോഴാണ് സമമിതി തകര്ച്ച (Symmetry Breaking) ഉണ്ടായി നാല് ബലങ്ങളും വേര്പ്പെട്ടത് എന്ന് പറയും.